aquí os dejo colgado un powerpoint sobre los sistemas de ecuaciones: pincha AQUÍ
miércoles, 22 de mayo de 2013
martes, 9 de abril de 2013
MATEMÁTICAS 3º DIVERSIFICACIÓN
PROGRAMA DEL CURSO 2012-2013.
1. REPASO: CONOCIMIENTOS MATEMÁTICOS BÁSICOS.
2. NÚMEROS REALES.
3. VARIABLES ESTADÍSTICAS.
4. PROBABILIDAD.
5. ECUACIONES Y SISTEMAS. LENGUAJE ALGEBRAICO.
6. SUCESIONES.
9. FUNCIONES MATEMÁTICAS.
LOS NÚMEROS REALES: INTRODUCCIÓN1
Tenéis que tener claro que un número real es.....
podéis ver este vídeo:
Actividad 1 PDF
Actividad2 interactiva
Realizar los siguientes ejercicios
Ejercicio 1. El número de hermanos de los alumnos de una clase es el siguiente:
0 1 0 0 3 2 1 4 0 0 1 1 2 0 1
1 2 0 1 1 2 1 3 0 0 2 1 2 3 5
a) Efectúa el recuento.
a) Efectúa el recuento.
b) Elabora una tabla de frecuencias.
c) Calcula: la media, la moda, la frecuencia relativa, la frecuencia acumulada, la mediana, la varianza, la desviación típica, la desviación media, el ángulo (para el diagrama de sectores), el rango, el coeficiente de variación.
d) Realiza el diagrama de barras y el polígono de frecuencias.
Ejercicio 2. En la siguiente tabla se recoge el número de veces que un grupo de usuarios de un ambulatorio han tenido que acudir a su médico en el último año.
Nº de visitas al médico
|
Nº de personas
|
1
|
10
|
3
|
25
|
5
|
43
|
7
|
31
|
10
|
12
|
12
|
4
|
a) Calcula: la media, la moda, la frecuencia relativa, la frecuencia acumulada, la mediana, la varianza, la desviación típica, la desviación media, el ángulo (para el diagrama de sectores), el rango, el coeficiente de variación.
b) Realiza el diagrama de barras y el polígono de frecuencias.
Ejercicio 3. La siguiente gráfica recoge la cantidad de parejas de zapatos vendidas en una tienda a lo largo del día:
a) Indica el tipo de gráfico.
b) Elabora una tabla de frecuencias.
c) Calcula: la media, la moda, la frecuencia relativa, la frecuencia acumulada, la mediana, la varianza, la desviación típica, la desviación media, el ángulo (para el diagrama de sectores), el rango, el coeficiente de variación.
Ejercicio 4. En un control de velocidad en carretera se obtuvieron los siguientes datos:
Datos: velocidad
Frecuencia absoluta: el número de coches
a) Calcula: la media, la moda, la clase modal, la frecuencia relativa, la frecuencia acumulada, la mediana, la varianza, la desviación típica, la desviación media, el ángulo (para el diagrama de sectores), el rango, la amplitud del intervalo y el coeficiente de variación.
b) Realiza el histograma y el polígono de frecuencias.
Ejercicio 5. La siguiente gráfica recoge las horas de estudio semanal de un grupo de alumnas y alumnos:
a) Indica el tipo de gráfico.
b) Elabora una tabla de frecuencias.
c) Calcula: la media, la moda, la clase modal, la frecuencia relativa, la frecuencia acumulada, la mediana, la varianza, la desviación típica, la desviación media, el ángulo (para el diagrama de sectores), el rango, la amplitud del intervalo y el coeficiente de variación.
Números naturales
N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ...}
1 Contar los elementos de un conjunto (número cardinal).
Ejemplo: 8 es el número de planetas del Sistema Solar.
Ejemplo: El pez verde es el segundo (2º) de los tres peces.
Ejemplo: Mi número de socio en el carnet del Club de vela es 40257.
Ejemplo: 5 > 3 
5 es mayor que 3.
3 < 5 3 es menor que 5.
Los números naturales son ilimitados, si a un número natural le sumamos 1, obtenemos otro número natural. 5 es mayor que 3. 3 < 5
3 es menor que 5. Representación de los números naturales
Sobre una recta señalamos un punto, que marcamos con el número cero (0).
A la derecha del cero, y con las mismas separaciones, situamos de menor a mayor los siguientes números naturales: 1, 2, 3...
Prioridad de las operaciones
2 Calcular las potencias y raíces.
3 Efectuar los productos y cocientes.
4 Realizar las sumas y restas.
Tipos de operaciones combinadas
- Sin paréntesis
- Con paréntesis
- Con corchetes
- Con llaves
1. Operaciones combinadas sin paréntesis
1.1 Combinación de sumas y diferencias
9 − 7 + 5 + 2 − 6 + 8 − 3 = 8
Comenzando por la izquierda, vamos efectuando las operaciones según aparecen.
1.2 Combinación de sumas, restas y productos
3 · 2 − 5 + 4 · 3 − 8 + 5 · 3 =
= 6 − 5 + 12 − 8 + 15 = 20
= 6 − 5 + 12 − 8 + 15 = 20
Realizamos primero los productos por tener mayor prioridad.
Posteriormente efectuamos las sumas y restas.
1.3 Combinación de sumas, restas, productos y divisiones
10 : 2 + 5 · 3 + 4 − 5 · 2 − 8 + 4 · 2 − 20 : 4 =
= 5 + 15 + 4 − 10 − 8 + 8 − 5 = 9
= 5 + 15 + 4 − 10 − 8 + 8 − 5 = 9
Realizamos los productos y cocientes en el orden en el que los encontramos porque las dos operaciones tienen la misma prioridad.
Efectuamos las sumas y restas.
1.4 Combinación de sumas, restas, productos, divisiones y potencias
23 + 10 : 2 + 5 · 3 + 4 − 5 · 2 − 8 + 4 · 22 − 20 : 4 =
= 8 + 10 : 2 + 5 · 3 + 4 − 5 · 2 − 8 + 4 · 4 − 20 : 4 =
= 8 + 5 + 15 + 4 − 10 − 8 + 16 − 5 = 25
= 8 + 10 : 2 + 5 · 3 + 4 − 5 · 2 − 8 + 4 · 4 − 20 : 4 =
= 8 + 5 + 15 + 4 − 10 − 8 + 16 − 5 = 25
Realizamos en primer lugar las potencias por tener mayor prioridad.
Seguimos con los productos y cocientes.
Efectuamos las sumas y restas.
Suma de números naturales
a + b = c
Los términos que intervienen en una suma se denominan:
a y b se denomina sumandos.
El resultado (c) se denomina suma.
Propiedades de la suma de números naturales
1 Operación interna
El resultado de sumar dos números naturales es otro número natural.
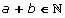
El resultado de sumar dos números naturales es otro número natural.
2 Asociativa
El modo de agrupar los sumandos no varía el resultado.
El modo de agrupar los sumandos no varía el resultado.
(a + b) + c = a + (b + c)
Ejemplo:
(2 + 3) + 5 = 2 + (3 + 5)
5 + 5 = 2 + 8
10 = 10
5 + 5 = 2 + 8
10 = 10
3 Conmutativa
El orden de los sumandos no varía la suma.
4 Elemento neutro El orden de los sumandos no varía la suma.
a + b = b + a
Ejemplo:
2 + 5 = 5 + 2
7 = 7
7 = 7
El 0 es el elemento neutro de la suma, porque todo número sumado con él da él mismo número.
a + 0 = 0 + a
Ejemplo:
a + 0 = a
3 + 0 = 3
3 + 0 = 3
Resta de números naturales
a − b = c
Los términos que intervienen en una resta se denominan:
a se denomina minuendo.
b se denomina sustraendo.
El resultado (c) se denomina diferencia.
a se denomina minuendo. b se denomina sustraendo. El resultado (c) se denomina diferencia.Propiedades de la resta de números naturales
1 No interna
El resultado de restar dos números naturales no siempre es otro número natural.
2 No conmutativa
Multiplicación de números naturales
Por ejemplo, la multiplicación 2·5 consiste en sumar el número 2 cinco veces.
a · b = c
Los términos que intervienen en una multiplicación se denominan:
a y b se denomina factores
El resultado (c) se denomina producto
a y b se denomina factores El resultado (c) se denomina productoPropiedades de la multiplicación de números naturales
1 Operación interna
El resultado de multiplicar dos números naturaleses otro número natural.
2 Asociativa
El modo de agrupar los factores no varía el resultado.
(a · b) · c = a · (b · c)
Ejemplo:
(2 · 3) · 5 = 2 · (3 · 5)
6 · 5 = 2 · 15
30 = 30
6 · 5 = 2 · 15
30 = 30
3 Conmutativa
El orden de los factores no varía el producto.
a · b = b · a
Ejemplo:
2 · 5 = 5 · 2
10 = 10
10 = 10
4 Elemento neutro
El 1 es el elemento neutro de la multiplicación de números naturales porque todo número multiplicado por él da el mismo número.
a · 1 = 1 · a = a
Ejemplo:
3 · 1 = 1 · 3 = 3
5 Distributiva
La multiplicación de un número natural por una suma es igual a la suma de las multiplicaciones de dicho número natural por cada uno de los sumandos.
a · (b + c) = a · b + a · c
Ejemplo:
2 · (3 + 5) = 2 · 3 + 2 · 5
2 · 8 = 6 + 10
16 = 16
2 · 8 = 6 + 10
16 = 16
6 Sacar factor común
Es el proceso inverso a la propiedad distributiva.
Si varios sumandos tienen un factor común, podemos transformar la suma en producto extrayendo dicho factor.
a · b + a · c = a · (b + c)
Ejemplo:
2 · 3 + 2 · 5 = 2 · (3 + 5)
6 + 10 = 2 · 8
16 = 16
6 + 10 = 2 · 8
16 = 16
División de números naturales
D : d = c
Los términos que intervienen en una división se denominan:
D se denomina dividendo
d se denomina divisor
El resultado (c) se denomina cociente
D se denomina dividendo d se denomina divisor El resultado (c) se denomina cocienteTipos de divisiones
D = d · c
Ejemplo:
D = d · c + r
Ejemplo:
Propiedades de la división de números naturales
Ejemplo:
2 : 6 
Ejemplo:
6 : 2 ≠ 2 : 6
Ejemplo:
0 : 5 = 0
Ejercicios
Realizar los siguientes ejercicios con operaciones combinadas:
1
8 − 6 + 7 − 5 − 2 + 8 − 6 =
2
4 · 3 − 8 + 7· 2 − 10 + 2 · 6 =
3
6 · 3 − 12 : 2 + 7 - 4 · 3 =
4
3² − 4 · 2 + 18 : 3 + 24 − 42 =
5
(13 − 4 · 2) − 4 + (2 · 6 − 7) − (14 − 3²) =
6
[3³ − (4 · 3 + 8)] − (3 · 6 − 15) + 22 - (8 − 6) =
7
8² − [(12 : 2) · (24 : 6)] − {25 − [24 − (18 : 3)]} =
TEMA 2: ESTADÍSTICA Y PROBABILIDAD
ACTIVIDADES
1. Indica que variables son cualitativas y cuales cuantitativas:
1 Comida Favorita.
2 Profesión que te gusta.
3 Número de goles marcados por tu equipo favorito en la última temporada.
4 Número de alumnos de tu Instituto.
5 El color de los ojos de tus compañeros de clase.
6 Coeficiente intelectual de tus compañeros de clase.
2. De las siguientes variables indica cuáles son discretas y cuales continuas.
1 Número de acciones vendidas cada día en la Bolsa.
2Temperaturas registradas cada hora en un observatorio.
3 Período de duración de un automóvil.
4 El diámetro de las ruedas de varios coches.
5 Número de hijos de 50 familias.
6 Censo anual de los españoles.
3. Clasificar las siguientes variables en cualitativas y cuantitativas discretas o continuas.
1 La nacionalidad de una persona.
2 Número de litros de agua contenidos en un depósito.
3 Número de libros en un estante de librería.
4 Suma de puntos tenidos en el lanzamiento de un par de dados.
5 La profesión de una persona.
6 El área de las distintas baldosas de un edificio.
4. Las puntuaciones obtenidas por un grupo en una prueba han sido:
15, 20, 15, 18, 22, 13, 13, 16, 15, 19, 18, 15, 16, 20, 16, 15, 18, 16, 14, 13.
Construir la tabla de distribución de frecuencias y dibuja el polígono de frecuencias.
5. El número de estrellas de los hoteles de una ciudad viene dado por la siguiente serie:
3, 3, 4, 3, 4, 3, 1, 3, 4, 3, 3, 3, 2, 1, 3, 3, 3, 2, 3, 2, 2, 3, 3, 3, 2, 2, 2, 2, 2, 3, 2, 1, 1, 1, 2, 2, 4, 1.
Construir la tabla de distribución de frecuencias y dibuja el diagrama de barras.
6. Las calificaciones de 50 alumnos en Matemáticas han sido las siguientes:
5, 2, 4, 9, 7, 4, 5, 6, 5, 7, 7, 5, 5, 2, 10, 5, 6, 5, 4, 5, 8, 8, 4, 0, 8, 4, 8, 6, 6, 3, 6, 7, 6, 6, 7, 6, 7, 3, 5, 6, 9, 6, 1, 4, 6, 3, 5, 5, 6, 7.
Construir la tabla de distribución de frecuencias y dibuja el diagrama de barras.
7. Los pesos de los 65 empleados de una fábrica vienen dados por la siguiente tabla:
| Peso | [50, 60) | [60, 70) | [70, 80) | [80,90) | [90, 100) | [100, 110) | [110, 120) |
| fi | 8 | 10 | 16 | 14 | 10 | 5 | 2 |
1 Construir la tabla de frecuencias.
2 Representar el histograma y el polígono de frecuencias.
8. Los 40 alumnos de una clase han obtenido las siguientes puntuaciones, sobre 50, en un examen de Física.
3, 15, 24, 28, 33, 35, 38, 42, 23, 38, 36, 34, 29, 25, 17, 7, 34, 36, 39, 44, 31, 26, 20, 11, 13, 22, 27, 47, 39, 37, 34, 32, 35, 28, 38, 41, 48, 15, 32, 13.
1 Construir la tabla de frecuencias.
2 Dibujar el histograma y el polígono de frecuencias.
9. Sea una distribución estadística que viene dada por la siguiente tabla:
| xi | 61 | 64 | 67 | 70 | 73 |
| fi | 5 | 18 | 42 | 27 | 8 |
Calcular:
1 La moda, mediana y media.
2 El rango, desviación media, varianza y desviación típica.
10.Calcular la media, la mediana y la moda de la siguiente serie de números: 5, 3, 6, 5, 4, 5, 2, 8, 6, 5, 4, 8, 3, 4, 5, 4, 8, 2, 5, 4.
11 Hallar la varianza y la desviación típica de la siguiente serie de datos:
12, 6, 7, 3, 15, 10, 18, 5.
12 Hallar la media, mediana y moda de la siguiente serie de números:
3, 5, 2, 6, 5, 9, 5, 2, 8, 6.
13. Hallar la desviación media, la varianza y la desviación típica de la series de números siguientes:
2, 3, 6, 8, 11.
12, 6, 7, 3, 15, 10, 18, 5.
14 Se ha aplicado un test a los empleados de una fábrica, obteniéndose la siguiente tabla:
| fi | |
| [38, 44) | 7 |
| [44, 50) | 8 |
| [50, 56) | 15 |
| [56, 62) | 25 |
| [62, 68) | 18 |
| [68, 74) | 9 |
| [74, 80) | 6 |
Dibujar el histograma y el polígono de frecuencias acumuladas.
15. Dadas las series estadísticas:
3, 5, 2, 7, 6, 4, 9.
3, 5, 2, 7, 6, 4, 9, 1.
Calcular:
La moda, la mediana y la media.
La desviación media, la varianza y la desviación típica.
Los cuartiles 1º y 3º.
Los deciles 2º y 7º.
Los percentiles 32 y 85.
16. Una distribución estadística viene dada por la siguiente tabla:
| [10, 15) | [15, 20) | [20, 25) | [25, 30) | [30, 35) | |
| fi | 3 | 5 | 7 | 4 | 2 |
Hallar:
La moda, mediana y media.
El rango, desviación media y varianza.
Los cuartiles 1º y 3º.
Los deciles 3º y 6º.
Los percentiles 30 y 70.
17. Dada la distribución estadística:
| [0, 5) | [5, 10) | [10, 15) | [15, 20) | [20, 25) | [25, ∞) | |
| fi | 3 | 5 | 7 | 8 | 2 | 6 |
Calcular:
La mediana y moda.
Cuartil 2º y 3º.
Media.
PROBABILIDAD
La rama de las matemáticas que se dedica al estudio de los procesos aleatorios es la probabilidad.
Cuando no conocemos con certeza el resultado de un experimento y al repetir dicho experimento el resultado no es el mismo, siempre que lo repitamos en las mismas condiciones estamos ante un experimento aleatorio.
Si, por el c ontrario, podemos predecir el resultado de un experimento, siempre que lo realicemos en las mismas condiciones, estamos hablando de un experimento determinista.
Al conjunto de todos los posibles resultados, se le denomina espacio muestral.
Ejercicios de probabilidad
Ejercicio 1. Lanzamos un dado con forma de dodecaedro con las caras numeradas del 1 al 12 y anotamos el número obtenido.
a) ¿Cuál es el espacio muestral?
b) Escribe los sucesos:
A = “Menos de 5”; B = “Más de 4”
C = “Número par”; D = “No múltiplo de 3”
Ejercicio 2. En una bolsa hay 6 bolas rojas, 4 azules, 7 verdes, 2 amarillas y una negra. Extraemos una al azar. Halla la probabilidad de que:
a) Sea azul.
b) No sea negra.
c) Sea verde.
d) Sea amarilla.
Ejercicio 3. Tenemos un dado de seis caras numeradas del 1 al 6. Indica el espacio muestral, los elementos que contienen cada suceso y la probabilidad de cada uno de ellos.
a) El resultado es múltiplo de 3.
b) El resultado es múltiplo de 2.
c) El resultado es mayor que 1.
d) El resultado es menor que 5.
e) El resultado es menor que 1.
Ejercicio nº 1.-
¿Qué es una experiencia aleatoria? De las siguientes experiencias ¿cuáles son aleatorias? a Al lanzar un dado sacar puntuación par. b Lanzar un dado y sacar una puntuación mayor que 6. c Bajar a la planta baja en ascensor.
Ejercicio nº 2 ¿Qué es una experiencia aleatoria? De las siguientes experiencias ¿cuáles son aleatorias? a En una caja hay cinco bolas amarillas, sacamos una bola y anotamos su color. b Lanzamos una moneda al aire y anotamos si sale cara o cruz. c Al lanzar un dado de seis puntos anotamos todos los resultados mayores que ocho.
Ejercicio nº 3.- ¿Qué es una experiencia aleatoria? De las siguientes experiencias ¿cuáles son aleatorias? a En una caja hay cinco bolas de diferentes colores, sacamos una y anotamos su color. b Hago girar la flecha de una ruleta con 4 colores y anoto el color que sale. c Rebeca anota todos los días si amanece.
Ejercicio nº 4.- ¿Qué es una experiencia aleatoria? De las siguientes experiencias ¿cuáles son aleatorias? a Mañana se pondrá el sol. b Me tocará la lotería. c Acertaré jugando a pares o nones.
Ejercicio nº 5.- ¿Qué es una experiencia aleatoria? De las siguientes experiencias ¿cuáles son aleatorias? a En una bolsa metemos seis bolas rojas y seis azules, sacamos una y anotamos su color. b Al lanzar una moneda al aire sale cara o cruz. c Al extraer una carta de la baraja observamos si sale un As.
Ejercicio nº 6.-En una urna hay 5 bolas, cuatro rojas y una azul, sacamos una bola y anotamos su color. Escribe el espacio muestral y califica cada suceso según su probabilidad:
TIPO DE SUCESO SUCESO
Seguro Sacar bola roja o azul.
Sacar bola azul.
Sacar bola verde.
Sacar bola roja.
Ejercicio nº 7.- Al lanzar un dado anotamos la puntuación obtenida. Escribe el espacio muestral y califica cada suceso según su probabilidad:
TIPO DE SUCESO SUCESO
Suceso Seguro Sacar una puntuación inferior a 7.
Sacar un 5.
Sacar un 7.
Sacar menos de 5.
Sacar más de 4.
TEMA 3 : LENGUAJE ALGEBRAICO, POLINOMIOS Y ECUACIONES
Término algebraico y sus partes
Se llama término a toda expresión algebraica cuyas partes no están separadas por los signos + o -. Así, por ejemplo xy2 es un término algebraico.
En todo término algebraico pueden distinguirse cuatro elementos: el signo, el coeficiente, la parte literal y el grado.
-4x2
|
signo
|
exponente
|
coeficiente
|
base o literal
|
Signo
Los términos que van precedidos del signo + se llaman términos positivos, en tanto los términos que van precedidos del signo – se llaman términos negativos. Pero, el signo + se acostumbra omitir delante de los términos positivos; así pues, cuando un término no va precedido de ningún signo se sobreentiende de que es positivo.
Coeficiente
Se llama coeficiente al número o letra que se le coloca delante de una cantidad para multiplicarla. El coeficiente indica el número de veces que dicha cantidad debe tomarse como sumando. En el caso de que una cantidad no vaya precedida de un coeficiente numérico se sobreentiende que el coeficiente es la unidad.
Parte literal
La parte literal está formada por las letras que haya en el término.
Grado
El grado de un término con respecto a una letra es el exponente de dicha letra. Así, por ejemplo el término x3y2z, es de tercer grado con respecto a x, de segundo grado con respecto ay y de primer grado con respecto a x.
2.5 Clasificación de los términos algebraicos; semejantes ó no semejantes.
Los términos que tienen las mismas variables con los mismos exponentes se llaman términos semejantes.
Reducción de términos semejantes
Se llama reducción de términos semejantes a la operación que consiste en reemplazar varios términos semejantes por uno solo. En la reducción de términos semejantes pueden presentarse los tres casos siguientes:
a)Para reducir términos semejantes que tengan igual signo se suman los coeficientes anteponiendo a la suma el mismo signo que tienen todos los términos y a continuación se escribe la parte literal.
b)Para reducir varios términos semejantes que tengan distintos signos se reducen todos los términos positivos a un solo término y todos lo términos negativos a un solo término y se restan los coeficientes de los términos así obtenidos anteponiendo a la diferencia el signo del mayor y a continuación se escribe la parte literal.
Ejemplo
Reducir 5a -8a +a -6a + 21a
Reduciendo los positivos: 5a +a + 21a = 27a
Reduciendo los negativos: -8a -6a = -14a
Aplicando a los resultados obtenidos (27a y -14a), la regla del caso anterior, se tiene 27a -14a =13a
Tendremos: 5a -8a +a -6a + 21a= 13a
ECUACIONES DE PRIMER GRADO
Una ecuación de primer grado con una incógnita es una igualdad en la que figura una letra sin exponente y
que es cierta para un solo valor de la letra, a este valor se le llama solución de la ecuación.
Ejemplo : 2x+5 = 3x-1
La solución de la ecuación es x = 4 ya que 2
·4+5 = 13 y 3·4+1 = 13
La solución de la ecuación no es x = 3 ya que 2
3+5 = 11 y 3·3+1 = 10
En una ecuación se pueden distinguir varios elementos:
Incógnita – Es la letra que aparece en la ecuación.
Coeficientes – Son los números o fracciones que acompañan a la incógnita.
Términos independientes – Son los números o fracciones que no acompañan a la incógnita.
Primer miembro – Es todo lo que hay a la izquierda del signo igual.
Segundo miembro - Es todo lo que hay a la derecha del signo igual.
Ejemplo : 3x+3 = 7x +8
Incógnita x
Coeficientes
Términos independientes : 3 y 8.
Primer miembro
3x +3
Segundo miembro
7x+ 8
–RESOLUCIÓN DE ECUACIONES SENCILLAS
Para resolver ecuaciones de primer grado sencillas, es decir para encontrar la solución, se realizan los
ACTIVIDADES
1) ¿Es x = 3 solución de la ecuación 4x - 1 = 3x + 1?
2) ¿Es x = 4 solución de la ecuación 2x + 3 =4x - 5?
3) ¿Es x = -2 solución de la ecuación 2x - 3 =4x + 1?
4) ¿Es x = -2 solución de la ecuación 5x - 4 =-2x + 18?
Para resolver ecuaciones de primer grado sencillas, es decir para encontrar la solución, se realizan los
siguientes pasos:
1º PASO
Se colocan todos los términos que llevan incógnita en el primer miembro y todos los términos
independientes en el segundo miembro, teniendo en cuenta que cuando un término cambia de miembro
también cambia de signo.
2º PASO
Se agrupan los términos semejantes, es decir se agrupan todos los términos con incógnita del primer
miembro por un lado y todos los términos independientes del segundo miembro por otro lado.
3º PASO
Si la incógnita lleva coeficiente, se pasa al segundo miembro dividiendo, si la división no sale exacta
1. POLÍGONOS
se puede dejar el resultado en forma de fracción.
Ejemplo : Resolver la ecuación 5x + 6 – 4x = - 4 + 3x - 8
1º
5x – 4x - 3x= - 6 – 4 - 8
2º
- 2x = - 18
3º
x = -18/2
x = 9
ACTIVIDADES
5) Resuelve las siguientes ecuaciones:
a) 2x+10 = 16 b) 10x-8 = 8x c) 45x = 180+40x
d) 9x-1 = 107-3x e) 2x+3 = x-9 f) 4x-2 = x+10
g) 3x-7 = 17 h) 5x+8 = 7x-32 i) 2x+7-5x = 8+x-12
3 –RESOLUCIÓN DE ECUACIONES CON PARENTESIS
Para resolver ecuaciones de primer grado con paréntesis, es decir para encontrar la solución, se realizan los siguientes pasos:
1º
Si hay paréntesis se quitan aplicando la propiedad distributiva.
2º
Se colocan todos los términos que llevan incógnita en el primer miembro y todos los términos
independientes en el segundo miembro, teniendo en cuenta que cuando un término cambia de miembro también cambia de signo.
3º
Se agrupan los términos semejantes, es decir se agrupan todos los términos con incógnita del primer
miembro por un lado y todos los términos independientes del segundo miembro por otro lado.
4º
Si la incógnita lleva coeficiente, se pasa al segundo miembro dividiendo, si la división no sale exacta
se puede dejar el resultado en forma de fracción.
Ejemplo : Resolver la ecuación 5(2x + 3) – 4x = - 4 + 3(x – 4)
1º
10x + 15 – 4x = - 4 + 3x – 12
2º
10x – 4x – 3x = - 15 – 4 – 12
3º
3x = - 31
4º
x = -31/3
ACTIVIDADES
6) Resuelve las siguientes ecuaciones:
a) 3(x-1) = x+11 b) 3x+7 = 2(8+x) c) 5(4+x) = 7x-2
d) 5(3x+2) =8(9 - 2x) e) 38+7(x-3) = 9(x-1) f) 2(3x-7)+6 = 4x-3(2-2x)
g) 11x+4 = 3(1-2x)+1 h) 7(3x+2)-5(4x-3) = 4(x-2)+1
SISTEMAS DE ECUACIONES
Antes de ver cómo vamos a resolver un sistema de ecuaciones vamos a estudiar las identidades notables.
Una identida notable es una igualdad.
Hay tres tipos:
a) El cuadrado de una suma.
( a + b ) = a + 2ab +b
b) El cuadrado de una resta.
( a - b ) = a + b - 2ab
c) Suma por diferencia.
( a + b ) ( a - b) = a - b
ACTIVIDADES
1. Resuelve las siguientes identidades notables:
a) ( x+2) =
b) ( 2x -4 ) =
c) (x+5)( x-5) =
d) (x -3/2) =
e) ( 3x+5/4) =
f) ( x+7/2)-7/2)
2. Resuelve los siguientes sistemas de ecuaciones:
a) 4x+y = 8
2x-2y = -6
b) 3x+2y = 6
2x-4y = -12
c) 2x-5y = -2
4x+10y = 8
d) 2x-y = -1
x+y = 1
e) 3x -2y = -8
-x+2y = 4
f) -x +2y = 10
2x+4y = -4
g) 2x+y = 2
-4x-2y = -4
CLASIFICACIÓN DE LOS SISTEMAS DE ECUACIONES
Los sistemas se clasifican según el número de soluciones que tengan:
- Sistema compatible determinado: tiene una única solución.
- Sistema compatible indeterminado: tiene infinitas soluciones.
- Sistema incompatible:
- no tiene soluciones.
Los ejemplos resueltos que hemos visto son todos cpmpatibles determinados.
Los sistemas incompatibles son aquellos que, al resolverlos, nos dan ecuaciones imposibles, del tipo:
0 = 3
Los sistemas compatibles indeterminados son aquellos que, al resolverlos, nos dan identidades del tipo:
0 = 0
Actividades
1. Representa gráficamente los sistemas anteriores y determina la relación que exixte entre el número de soluciones y las rectas que has obtenido.
ACTIVIDADES
Resuelve los siguientes sistemas por el método que prefieras, indicando en cada caso si el sistema es incompatible, compatible determinado o compatible indeterminado:
a) 3x +2y = 1
-6x-4y x0 5
b) 2x - y = 4
3x + y = 1
c) 4x - y = 2
8x - 2y = 4
d) 6x - 8y = 14
3x - 4y = 6
e) 3x +y = 2
6x - 2y = 0
f) -3x + y = 2
6x - 2y = -4
RESOLUCIÓN DE PROBLEMAS
El lenguaje algebraico y las ecuaciones son la herramienta perfecta para resolver numerosos problemas. Para poder resolver estos problemas de la manera más efectiva es conveniente que desarrolles los siguientes pasos:
1. Lee atentamente el enunciado del problema. Para conseguir resolver un problema debes comprender perfectamente lo que te dice el enunciado.
2. Ordena la información que te da el enunciado. Determina claramente lo que sabes y lo que quieres saber.
3. Elige una incógnita. ¿Qué quieres saber? ¿Con qué letra lo representas?
4. Plantea la ecuación traduciendo los datos del problema a lenguaje algebraico.
5. Resuelve la ecuación.
6. Comprueba que tu solución responde a lo que planteaba el problema y si lo hace correctamente.
ACTIVIDADES.
1. Sabemos que para cercar una parcela rectangular hemos necesitado 150m de valllas. Si además sabemos que el largo de la parcela es tres veces el ancho, ¿cuáles son las dimensiones de la parcela?
2. Ana cobra un sueldo neto de 1325€. Si paga un IRPF del 20 %, ¿a cuánto asciende su sueldo bruto?
3. Si al comprar nueve camisas iguales me rebajan 3 € en el precio de cada camisa, y en total me gasto 216 €, ¿cuánto costaba una camisa antes de la rebaja?
4. Un padre quiere repartir 100 € entre sus tres hijos de forma que al primero le corresponda cuatro veces más que al segundo, y al tercero, lo mismo que a los otros dos juntos. ¿Cuánto debería darle acada uno?
5. Si tenemos 315 € en billetes de 5 €, 10 € y 20 €, de forma que tenemos el mismo número de billetes de los tres tipos, ¿cuántos billetes tenemos en total?
6. Encuentra dos números naturales consecutivos que sumados entre sí nos den un número que sea el triple del primero de ellos.
7. Durante la segunda evaluación, Ángel ha hecho dos examenes de Matemáticas. Su nota media es 6,5. Sabiendo que en el segundo examen obtuvo 2,5 puntos más que en el primero, ¿qué nota obtuvo Ángel en cada examen?
8. Las dos cifras de la edad de Isabel suman 7. Si a cinco veces la primera le restamos dos veces la segunda, obtenemos 21. ¿Cuántos años tiene Isabel?
9. El precio de un ordenador de segunda mano es cinco veces menor que el de uno nuevo. Si resulta que un ordenador viejo cuesta 720 € menos que uno a estrenar, ¿cuánto cuesta cada ordenador?
10. En una clase de 27 alumnos el número de chicas es el doble que el de chicos. ¿Cuántos chicos y chicas hay?
TEMA 4 : SUCESIONES
Otros elementos matemáticos que nos ayudan a estudiar y resolver numerosos problemas son las sucesiones.
Una sucesión es un conjunto ordenado de números, cada uno de los cuales recibe el nombre de término. De forma general, escribimos una sucesión como:
a1, a2, a3,......,an,....
donde hemos representado cada término con una a con un subíndice que nos indica el lugar que ocupa en la sucesión: a1 es el primer término de la sucesión, a2 el segundo, a3 el tercero..... y an es el término n-ésimo, también denominado término general.
Las sucesiones tienen aplicaciones muy variadas, ya que sirven para describir numerosas situaciones que van desde el número de individuos de una población año tras año hasta la evolución del precio de un valor de bolsa.
Para expresar una sucesión cualquiera se pueden utilizar varios métodos:
- Descripción de sus téminos: determinamos una sucesión mediante una propiedad que define sus términos. Ejemplos:
- Los números naturales pares: 2,4,6,8,.....
- Los múltiplos de 11: 11,22,33,44,.....
- Los números primos: 2,3,5,7,11,.....
- Ley de recurrencia: construimos cada término en relación a los anteriores. Tendremos que conocer también alguno de los primeros términos para poder empezar a calcular los demás. Ejemplos: an = 2.an-1 esw una ley de recurrencia que nos indica que cada término es el doble del anterior. Para poder aplicarla necesitamos un punto de partida que puede ser, por ejemplo, el primer término a1 = 3; con esto podemos escribir la sucesión: 3,6,12,24,48,.......
- Término general: podemos definir una sucesión mediante una expresión que relaciones el valor de cad término con la posición que ocupa.
Actividades
1. Escribe el término general de las siguientes sucesiones:
a) 3,5,7,9,11,13,.......
b) 0,3,8,15,24,.........
c) 1,4,9,16,25,........
d) 2,6,18,54,..........
e) 5,10,15,20,25,.......
f) 2,8,18,32,50,..........
g) 4,16,64,256,..........
h) 15,11,7,3,-1,.........
i) 2,9,28,65,126,......
2. Calcula el décimo término de todas las sucesiones anteriores.
3. Una sucesión viene definida por la ley de recurrencia an = 3.an-1 +2. Además sabemos que a1 = -4.
a) Calcula sus seis primeros términos.
b) Escribe su término general.
4. Dda una sucesión definida mediante el término general an = 2n +5:
a) Escribe sus cinco primeros términos.
b) Escribe el término duodécimo.
c) ¿Qué lugar ocupa en la sucesión el número 5?
5. Define las siguientes sucesiones mediante una ley de recurrrencia y alguno de sus términos:
a) 1,5,9,13,17,......
b) 1,0,1,0,01,,0,001,.....
c) 2,1,3,4,7,11,18,.....
d) 11,5,-1,-7,-13,.......
PROGRESIONES ARITMÉTICAS Y GEOMÉTRICAS
Son un tipo especial de sucesiones y son especialmente útiles por ser muy sencillas y aparecer en numerosos fenómenos; por ejemplo, las poblaciones de seres vivos tienden a multiplicarse siguiendo una progresión geométrica. También podrás descubrir elementos relacionados con estas sucesiones en numerosas obras de arte.
1. Progresiones aritméticas.
Son aquellas sucesiones en las que cada término se obtiene sumando al anterior un número fijo. Este número fijo recibe el nombre de diferencia (d).
Ejemplo: Dada la progresión aritmética 3 7 11 15 ....
En esta progresión a1= 3 y d = 4; su término general será:
an = 3 + (n-1).4 = 3 +4n-4 = 4n-1
Según esto el término n-ésimo:
an = a1 +( n-1).d
2. Progresiones geométricas.
Son aquellas sucesiones en las que obtenemos cada término multiplicando el anterior por un número fijo que denominamos razón(r).
De esta forma tendremos:
a1 = a1
a2 = a1.r
a3 = a2.r = a1.r.r = a1.r2
a4 = a3.r = a1.r.r.r = a1.r3
De aquí deducimos la expresión para el término general de una progresión geométrica cuyo primer término es a1 y su razón es r:
an = a1.rn-1
Ejemplo: 3 12 48 192......
a1= 3 y r = 4, así: an = 3.4n-1
ACTIVIDADES
1. En una progresión geométrica a1 = 5 y d = 7:
a) Escribe su término general.
b) Escribe sus cinco primeros términos.
c) Calcula su término número 100.
2. En una progresión geométrica a1 = 4 y r = 3:
a) Escribe su término general.
b) Escribe sus cinco primeros términos.
c) Calcula su término número 25.
3. Escribe el término general de las siguientes progresiones indicando en cada caso si se trata de una progresión aritmética o geométrica:
a) 1,2,3,4,5,6,.........
b) 2,4,8,16,32,........
c) 2,4,6,8,10,..........
d) 5,10,15,20,25,....
e) -1,1,-1,1,-1,.........
f) 8,5,2,-1,-4,..........
g) 3,-6,12,-24,48,...
h) 4,4/3,4/9,4/27,...
i) 1,3/2,2,5/2,3,......
4. En una progresión aritmética sabemos que a3 = 13 y a7 = 25.
a) Calcula la diferencia.
b) Escribe el término general.
c) Calcula a100.
5. En una progresión geométrica sabemos que a2 = 15 y a4 = 375.
a) Calcula la razón.
b) Escribe el término general.
Calcula a10.
NOTA.
1,2,4,8,16,32,64,128,.......
La progresión geométrica formada por las potencias de 2 tiene hoy un papel fundamental en nuestra sociedad. Todos los dispositivos electrónicos ( calculadoras,ordenadores,discos compactos.....) utilizan como lenguaje el sistema binario de numeración que tiene su base en esta sucesión.
TEMA 5 : CUERPOS GEOMÉTRICOS
Los contenidos de este tema son los siguientes:
- Polígonos. Cálculo de áreas.
- Teoremas. Pitágoras y Tales.
- Poliedros. Cálculo de volúmenes.
- Circunferencia y círculo.
- Cuerpos de revolución: cono, cílindro y esfera.
¿Qué sabes de esto?
- Enuncia el teorema de Pitágoras.
- ¿Qué es un polígono?
- ¿Cuál es la fórmula para hallar el área de la circunferencia?
- ¿Cuál es el área de una esfera?
1. POLÍGONOS
Un polígono es la parte del plano limitada por una línea poligonal cerrada.
Su clasificación se hace en base al número de lados:
- El de tres lados es un triángulo
- El de cuatro lados es un cuadrilátero
- El de cinco es un pentágono
- El de seis un hexágono, etc.
Los polígonos regulares tienen todos sus lados y ángulos iguales; si no es así, hablamos de polígonos irregulares.
Un polígono es convexo cuando tiene sus ángulos menores de 180º; y es cóncavo cuando tiene algún lado mayor de 180º.
TRIÁNGULOS
Un triángulo es un polígono que tiene tres lados. En un triángulo podemos distinguir:
Base: uno cualquiera de sus lados.
Altura: es el segmento perpendicular a un lado.
CLASIFICACIÓN DE LOS TRIÁNGULOS
Propiedades de los triángulos:
- Un lado cualquiera de un triángulo es siempre menor que la suma de los otros dos y mayor que su diferencia. Si no se cumple esta propiedad, no se puede dibujar un triángulo.
- La suma de los tres ángulos de un triángulo es 180º.
- Un triángulo es rectángulo si uno de sus ángulos es recto(90º). En estos triángulos, los lados perpendiculares se llaman catetos, y el lado opuesto, hipotenusa.
2. TEOREMAS
El teorema de Pitágoras dice así: " En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos". Es decir:
c2 = a2 + b2
El teorema de Tales: si tenemos dos rectas r y s y tres rectas paralelas A,B y C que las cortan, los segmentos que resulten sobre r y s son proporcionales.
AB/A'B' = AC/A'C' = BC/B'C'
3. CLASIFICACIÓN DE LOS CUADRILÁTEROS
Propiedades de los paralelogramos:
- Si trazamos una diagonal, el paralelogramo queda dividido en dos triángulos iguales.
- Los lados opuestos de un paralelogramo tiene la misma longitud.
- Los ángulos opuestos de un paralelogramo son iguales, mientras que los contiguos son suplementarios.
- Las diagonales de un paralelogramo se cortan en el punto medio de las dos.
Áreas de cuadriláteros y triángulos:
Cuadrado: A = ladoxlado
P = 4.l
Rectángulo y Romboide: A = basexaltura
P = 2b +2a
Poligono regular: A = perímetroxapotema/2
P = nº ladosxl
Rombo: A = diagonal mayorxdiagonalmenor/2
P = 4.l
Trapecio: A = B+b/2.h
P = B+b+l1+l2
Tiángulo: A = basexaltura/2
P = l1+l2+b
En un polígono, se denomina p´rímetro la suma de las longitudes de todos sus lados, y apotema, la distancia desde el punto medio hasta la base.
EJERCICIOS
1. Indica en tu cuaderno las diferencias que encuentres entre:
a) Un rombo y un rectángulo.
b) Un cuadrado y un rombo.
c) Un cuadrado y un trapecio.
d) Un tectángulo y un romboide.
e) Un cuadrado y un rectángulo.
f) Un rombo y un romboide.
2. Dibuja un hexágono regular de 6 cm de lado. Ayudándote con una regla graduada, consigue los datos que necesites para calcular su área.
3. Sabiendo que la suma de los ángulos de un polígono de n lados es 180º.(n-2), calcula cuánto suman los ángulos de un cuadrado, un pentágono, un hexágono y un octógono.
4. Calcula cuánto miden los lados de un cuadrado que tiene de área 9 cm2.
5. Un rectángulo tiene de área 24 cm2. Si la base mide 6 cm, ¿cuánto mide su altura? ¿Cuánto mide cada una de sus diagonales?
6. La diagonal mayor de un rombo mide 10 cm y su diagonal menor es 2/5 de la mayor. Calcula su área.
4. POLIEDROS
Un poliedro es un cuerpo geométrico limitado por caras que son polígonos. Reciben el nombre de aristas los lados comunes a dos caras, y vértices, los puntos donde se unen más de dos caras.
Prismas regulares:
- Tetraedro: tiene 4 caras de triángulos equiláteros.
- Octaedro: 8 caras de triángulos equiláteros.
- Icosaedro: 20 caras de triángulos equiláteros.
- Cubo: 6 caras de cuadrados.
- Dodecaedro: 12 caras de pentágonos regulares.
4.1 Prismas
Un prisma es un poliedro compuesto por dos caras paralelas formadas por polígonos iguales ( bases), mientras que el resto de sus caras son paralelogramos.
En un prisma se cumple:
- Si la base tiene n lados, el nº de caras es n+2.
- El número de aristas es 3.n y el número de vértices es 2.n
Combinando estos datos se obtiene la relación:
número de caras+número de vértices= número de aristas+2
4.2 Pirámides
Una pirámide es un poliedro cuya base es un polígono cualquiera y sus caras restantes son triángulos que concurren en un vértice.
En una pirámide se cumple:
- Si la base tiene n lados, el número de caras es n+1.
- El número de aristas es 2n y el número de vértices es n+1
Así, una pirámide cuadrangular cuya base es un cuadrado tendrá 5 caras, 8 aristas y 5 vértices.
Poliedro con base de n lados
|
Nº de caras
|
Nº de aristas
|
Nº de vértices
|
Prisma
|
n+2
|
3n
|
2n
|
Pirámide
|
n+1
|
2n
|
n+1
|
ACTIVIDADES
1. Completa en tu cuaderno la siguiente tabla:
Nombre del prisma
|
Nº de lados de la base
|
Nº de vértices
|
Nº de caras
|
Nº de aristas
|
3
| ||||
6
| ||||
P. pentagonal
|
12
|
15
| ||
7
| ||||
10
|
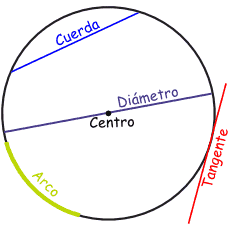
La circunferencia es una línea cerrada y plana, donde todos los puntos están a la misma distancia de un punto central llamado centro.
En una circunferencia podemos encontrar los siguientes segmentos:
- Radio: es el segmento que une el centro con un punto cualquiera de la circunferencia.
- Cuerda: es el segmento que une dos puntos cualesquiera de la circunferencia.
- Diámetro: es la cuerda que pasa por el centro. Equivale a dos veces el radio.
La circunferencia tiene una amplitud de 360º. Si dividieramos la circunferencia en cuatro cuadrantes, cada uno de ellos tendría un ángulo de 90º.
Ángulos:
- Nulo (0º)
- Recto (90º)
- Llano (180º)
- Completo (360º)
- Ángulo agudo: mide menos que un ángulo recto.
- Ángulo obtuso: mide más que un ángulo llano.
5.1 Longitud de la circunferencia.
Se calcula multiplicando el diámetro por el número pi, tomando este como 3,14.
L = 2 πr
5.2 Área del círculo.
Ya hemos visto que la circunferencia es una línea, pero en su interior encierra una superficie llamada círculo.
Un sector circular es la región del plano comprendida entre dos radios.
El área de un círculo de radio r es igual al producto de pi por el radio al cuadrado.
S = π.r²
5.3 Área de la corona circular.
Si tenemos dos circunferencias, una dentro de otra, la mayor de radio R y la menor de radio r, el área de la corona circular se obtiene al restar el área del círculo menor del área del círculo mayor.
S = π.( R²- r²)
ACTIVIDADES
1. Dibuja en tu cuaderno una circunferencia que contenga: el radio, la cuerda y el diámetro.
2. Calcula la longitud de una circunferencia de 8 cm de diámetro.
3. Una circunferencia tiene una longitud de 314 cm. Halla su radio y su diámetro.
4. El radio de un círculo mide 5 cm. Calcula su área en metros cuadrados.
5. Calcula el área de una corona circular determinada por dos circunferencias de radios 7 cm y 10 cm.
6. ¿Qué radio tiene un círculo si su área mide 60 cm cuadrados?
7. ¿Qué diferencia hay entre una circunferencia y un círculo.?
8. Dibuja en tu cuaderno una corona circular cuyo radio menor mida 4 cm, y el mayor, 6cm. Calcula el área de dicha corona circular.
6. CUERPOS DE REVOLUCIÓN
Se llaman así porque se obtienen girando una figura plana alrededor de un eje.
6.1 Cilindro.
Se obtiene al girar un rectángulo alrededor de un lado. En el se distinguen:
- La generatriz (g): su medida coincide con la altura del cilindro.
- La altura (h): es el segmento que une los centros de las dos circunferencias o bases.
- El radio (r).
6.2 Cono.
Se obtiene al girar un triángulo alrededor de un cateto. Al igual que en el cilindro podemos distinguir generatriz, altura y radio.
6.3 Esfera.
Se obtiene al girar un semicírculo alrededor de su diámetro. En una esfera se distinguen: diámetro, radio y centro.
ÁREAS Y VOLÚMENES DE CUERPOS DE REVOLUCIÓN
CILINDRO
Al = 2.π.R
At = Al + 2.Ab
V = Ab . altura
CONO
Al = π.R.g
At = Al + Ab
V = 1/3.Ab.altura
ESFERA
A = 4.π.R2
V = 4/3.π.R3
Al = 2.π.R
At = Al + 2.Ab
V = Ab . altura
CONO
At = Al + Ab
V = 1/3.Ab.altura
ESFERA
V = 4/3.π.R3
Actividades
2.- ¿Cuál es el volumen de un cilindro de 1 cm de radio y 1 cm de altura o generatriz?. Varía el valor de laaltura desde 1 hasta 3 cm, de 0,5 en 0,5 cm.
3.- Halla los volúmenes de cilindros cuya alturas es de 1 cm y con radios: 1; 1,25; 1,5 y 2 cm, respectivamente.
4.- Repite las actividades 2 y 3 para una altura de 2 cm.
5.- Intenta hallar una expresión que permita calcular el volumen de un cilindro, conocidos su radio y su altura.
6.- Comprueba la validez de la expresión hallada en la actividad anterior calculando los volúmenes de los cilindros de la actividad 3.
7.- Calcula la altura de un depósito cilíndrico de 3 m de radio y 282,6 m3 de volumen. Si ese volumen fuera el volumen interior, ¿cuántos litros de agua se podrían almacenar en dicho depósito?
Ejercicios.
2Una piscina tiene 8 m de largo, 6 m de ancho y 1.5 m de profundidad. Se pinta la piscina a razón de 6 € el metro cuadrado.
1Cuánto costará pintarla.
2Cuántos litros de agua serán necesarios para llenarla.
3En un almacén de dimensiones 5 m de largo, 3 m de ancho y 2 m de alto queremos almacenar cajas de dimensiones 10 dm de largo, 6 dm de ancho y 4 dm de alto. ¿Cuantas cajas podremos almacenar?4Determina el área total de un tetraedro, un octaedro y un icosaedro de 5 cm de arista.
5 Calcula la altura de un prisma que tiene como área de la base 12 dm2 y 48 l de capacidad.
6 Calcula la cantidad de hojalata que se necesitará para hacer 10 botes de forma cilíndrica de 10 cm de diámetro y 20 cm de altura.
7Un cilindro tiene por altura la misma longitud que la circunferencia de la base. Y la altura mide 125.66 cm. Calcular:
1 El área total.
2 El volumen
8En una probeta de 6 cm de radio se echan cuatro cubitos de hielo de 4 cm de arista. ¿A qué altura llegará el agua cuando se derritan? 9 La cúpula de una catedral tiene forma semiesférica, de radio 50 m. Si restaurarla tiene un coste de 300 € el m2, ¿A cuánto ascenderá el presupuesto de la restauración?
10¿Cuántas losetas cuadradas de 20 cm de lado se necesitan para recubrir las caras de una piscina de 10 m de largo por 6 m de ancho y de 3 m de profundidad?
11Un recipiente cilíndrico de 10 cm de radio y y 5 cm de altura se llena de agua. Si la masa del recipiente lleno es de 2 kg, ¿cuál es la masa del recipiente vacío?
12Para una fiesta, Luís ha hecho 10 gorros de forma cónica con cartón. ¿Cuánto cartón habrá utilizado si las dimensiones del gorro son 15 cm de radio y 25 cm de generatriz?
13Un cubo de 20 cm de arista está lleno de agua. ¿Cabría esta agua en una esfera de 20 cm de radio?
TEMA6: TRANSFORMACIONES GEOMÉTRICAS
Las transformaciones geométricas se dividen en:
- Traslaciones
- Giros
- Simetrías:pueden ser central y axial.
- Semejanzas: estas se aplican en la vida real mediante escala.
Se aplican en el plano cocordenado.
1.El plano.
1.1. Puntos en el plano.
En esta unidad vamos a estudiar cómo aplicar determinadas transformaciones sobre puntos situados EN EL PLANO. Para ello vamos a construir un sistema de cocrdenadas que está formado por dos rectas perpendiculares entre sí. El eje horizontal recibe el nombre de eje X o eje de abscisas, y la vertical, eje Y o eje de ordenadas.
El punto en el que se cortan se denomina origen.
Cada punto está determinado por dos coordenadas P(x,y).
1.2. Vectores.
Un vector fijo 
es un segmento orientado que va del punto A (origen) al punto B (extremo).
es un segmento orientado que va del punto A (origen) al punto B (extremo).Elementos de un vector
Dirección de un vector
La direcccíon del vector es la dirección de la recta que contiene al vector o de cualquier recta paralela a ella.
Sentido de un vector
El sentido del vector 
es el que va desde el origen A al extremo B.
es el que va desde el origen A al extremo B.Módulo de un vector
El módulo del vector es la longitud del segmento AB, se representa por 
.
es la longitud del segmento AB, se representa por .
El módulo de un vector es un número siempre positivo o cero.
Módulo de un vector a partir de sus componentes
Módulo a partir de las coordenadas de los puntos
Coordenadas de un vector
Si las coordenadas de los puntos extremos, A y B, son:
Las coordenadas del vector son las coordenadas del extremo menos las coordenadas del origen.
son las coordenadas del extremo menos las coordenadas del origen.
Clases de vectores
Vectores equipolentes
Dos vectores son equipolentes cuando tienen igual módulo, dirección y sentido.
Vectores libres
El conjunto de todos los vectores equipolentes entre sí se llama vector libre. Es decir los vectores libres tienen el mismo módulo, dirección y sentido.
Vectores fijos
Un vector fijo es un representante del vector libre. Es decir, los vectores fijos tienen el mismo módulo, dirección, sentido y origen.
Vectores ligados
Los vectores ligados son vectores equipolentes que actúan en la misma recta. Es decir, los vectores fijos tienen el mismo módulo, dirección, sentido y se encuentran en la misma recta.
Vectores opuestos
Los vectores opuestos tienen el mismo módulo, dirección, y distinto sentido.
Vectores unitarios
Los vectores untario tienen de módulo, la unidad.
Para obtener un vector unitario, de la misma dirección y sentido que el vector dado se divide éste por su módulo.
Vectores concurrentes
Los vectores concurrentes tienen el mismo origen.
Vector de posición
El vector 
que une el origen de coordenadas O con un punto P se llama vector de posición del punto P.
que une el origen de coordenadas O con un punto P se llama vector de posición del punto P.Vectores linealmente dependientes
Varios vectores libres del plano son linealmente dependientes si existe una combinación lineal de ellos que sea igual al vector cero, sin que sean cero todos los coeficientes de la combinación lineal.
Vectores linealmente independientes
Varios vectores libres son linealmente independientes si ninguno de ellos se puede expresar como combinación lineal de los otros.
a1 = a2 = ··· = an = 0
Vectores ortogonales
Dos vectores son ortogonales o perpendiculares si su producto escalar es cero.
Vectores ortonormales
Dos vectores son ortonormales si:
1. Su producto escalar es cero.
2. Los dos vectores son unitarios.
Actividades sobre vectores:
Vectores. Producto escalar. Ejercicios
1Hallar el simétrico del punto A(4, - 2) respecto de M(3, - 11).
2Dados dos vértices de un triángulo A(2, 1), B(1, 0) y el baricentro G(2/3, 0), calcular el tercer vértice.
3Dados los puntos A (3, 2) y B(5, 4) halla un punto C, alineado con A y B, de manera que se obtenga
4Calcula las coordenadas de D para que el cuadrilátero de vértices: A(-1, -2), B(4, -1), C(5, 2) y D; sea un paralelogramo.
5 Si {
, 
} forma una base ortonormal, calcular:
=(2, k) y = (3, - 2), calcula k para que los vectores y sean:
8 Suponiendo que respecto de la base ortonormal { , } del plano los vectores 
tienen como expresiones:
sobre el vector 
.
10 Hallar un vector unitariode la misma dirección del vector 
.
2Dados dos vértices de un triángulo A(2, 1), B(1, 0) y el baricentro G(2/3, 0), calcular el tercer vértice.
3Dados los puntos A (3, 2) y B(5, 4) halla un punto C, alineado con A y B, de manera que se obtenga
4Calcula las coordenadas de D para que el cuadrilátero de vértices: A(-1, -2), B(4, -1), C(5, 2) y D; sea un paralelogramo.
5 Si {
, } forma una base ortonormal, calcular:
1 ·
·
2 ·
·
3 ·
·
4 ·
6 Dados los vectores · =(2, k) y = (3, - 2), calcula k para que los vectores y sean:
1 Perpendiculares.
2 Paralelos.
3 Formen un ángulo de 60°.
7 Calcular el valor de k sabiendo que , } del plano los vectores tienen como expresiones:
Calcular el valor de k para que los dos vectores sean ortogonales.
9 Calcula la proyección del vector sobre el vector .10 Hallar un vector unitario
de la misma dirección del vector .
Transformaciones
Los tres tipos principales de transformaciones son:
| Rotaciones | 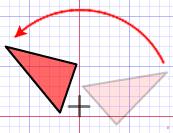 | ¡Girar! |
|---|---|---|
| Reflexiones | 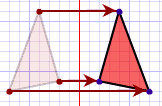 | ¡Voltear! |
| Translaciones | 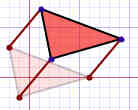 | ¡Deslizar! |
 | Después de hacer estas transformaciones (girar, voltear o deslizar), la forma tiene el mismo tamaño, área, ángulos y longitudes. |
 | Si una forma se puede convertir en otra usando giros, volteos y deslices, las dos formas se llaman congruentes. |
Cambiar tamaño
La otra transformación importante es la homotecia (también llamada dilatación, contracción, compresión, alargamiento o expansión). La forma se hace más grande o más pequeña:| Homotecia | 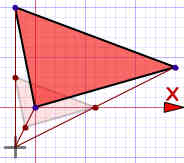 | ¡Cambio de tamaño! |
|---|
Actividades
La traslación es una transformación puntual por la cual a todo punto A del plano le corresponde otro punto A' también del plano de forma que 
. Siendo 
el vector que define la traslación.
. Siendo el vector que define la traslación.
La traslación se designa por 
, luego 
.
, luego .
El punto A' es el punto trasladado de A.
Un punto y su trasladado se dice que son homólogos.
Coordenadas de un punto mediante una traslación.
Traslación de una recta
Una recta se transforma, mediante una traslación, en una recta paralela.
Traslación de una circunferencia
La homóloga de una circunferencia mediante una traslación es otra circunferencia de igual radio que tiene como centro el punto homólogo del centro de la circunferencia original.
Una traslación en el plano está definida por un vector 
.
.
1 Hallar la imagen por dicha traslación de un punto A (1,3).
2 Hallar la transformada de una circunferencia que tiene de centro (3,4) y de radio 1
En una traslación mediante el vector , un punto A (3, - 2) se transforma en un punto A' (1,5). Calcular:
, un punto A (3, - 2) se transforma en un punto A' (1,5). Calcular:
El transformado del punto B(-2, 4).
La transformada de una circunferencia de centro (1,2).y radio 3.
Una traslación tiene de vector 
. Hallar la figura transformada de un triángulo cuyos vértices son:
. Hallar la figura transformada de un triángulo cuyos vértices son:
Composición de traslaciones
Al aplicar sucesivamente dos traslaciones de vectores 
, se obtiene otra traslación cuyo vector es la suma de los vectores:
, se obtiene otra traslación cuyo vector es la suma de los vectores:
Coordenadas mediante una simetría de centro O(0,0)
Un punto P' homólogo de un punto P(x,y) mediante una simetría central de centro O(0,0) tiene de coordenadas:
Una simetría de centro O equivale a un giro de centro O y amplitud 180°.
P' = (-x, -y)
x' = -x y' = -y
Coordenadas mediante una simetría de centro O(a, b)
Un punto P' homólogo de un punto P(x,y) mediante una simetría central de centro O(a ,b) tiene de coordenadas:
P' = (-x+ 2a, -y+ 2b)
x' = -x + 2a
y' = -y + 2b
Composición de simetrías centrales
Con el mismo centro
Como una simetría de centro O equivale a un giro de centro O y amplitud 180°, al aplicar otra transformación el ángulo será de 360°, por lo que se obtiene la misma figura, lo que se llama involución. Es una transformación involutiva.
Con distinto centro
La composición de dos simetrías centrales con distinto centro es una traslación.
Centro de simetría
Un punto es centro de simetría de una figura si define una simetría central.
Una simetría axial de eje e es una transformación, por tanto a todo punto P del plano le corresponde otro punto P' también del plano, de manera que el eje e sea la mediatriz del segmento AA'.
Las simetrías axiales son isometrías porque conservan las distancias entre los puntos y sus homólogos.
Coordenadas de puntos mediante simetrías axiales
Coordenadas de un punto simétrico al eje de ordenadas
Dos puntos A(x, y) y A'(x', y') simétricos respecto del eje de ordenadas tienen sus abscisas opuestas y sus ordenadas iguales.
P(x, y) 
P(-x, y)
P(-x, y)
x = -x' y = y'
Coordenadas de un punto simétrico al eje de abscisas
Dos puntos A(x, y) y A'(x', y') simétricos respecto del eje de abscisas tienen sus abscisas iguales y sus ordenadas opuestas.
P(x, y) P(x, -y)
P(x, -y)
x = x' y = -y'
Composición de simetrías axiales
Simetría de ejes paralelos
La composición de dos simetrías ejes paralelos e y e' es una traslación, cuyo vector tiene:
La longitud del vector es el doble de la distancia entre los ejes.
La dirección del vector es perpendicular a los ejes.
El sentido es el que va de e a e'.
Simetría de ejes perpendiculares
La composición de dos simetrías de ejes perpendiculares e y e' es una simetría central respecto del punto de corte de los dos ejes de simetría.
Eje de simetría
El eje de simetría de una figura es la recta que divide a la figura en dos partes iguales, de modo que define una simetría axial entre una parte y otra.
SEMEJANZA
- Mediante la equivalencia entre la unidad de medida en la representación y la realidad.
En ese caso tendríamos escalas del tipo 10:1 que nos indicaría que 10 cm de la maqueta o el dibujo representan 1 cm de la realidad.
- Mediante un segmento nos indica que cada una de las partes en las que está dividido equivalen a un metro de la realidad.
Actividades
1. Un grupo de alumnos decide hacer una maqueta de la torre de la iglesia de su pueblo. Esta torre mide 20 m de alto. Se plantean realizar la maqueta con una escala 1:50. ¿Cuál será la altura de la maqueta?
2. La torrre Eiffel de París mide 320 m de altura. En una tienda de souvenirs compramos una reproducción a escala que mide exactamente 16 cm de altura. ¿A qué escala está construida?
3. Para pintar las paredes de una maqueta realizada con una escala de 1:20 hemos gastado 20.... en pintura. ¿Cuánto dinero gastaremos en pintar el edificio real si la pintura que vamos a emplear cuesta lo mismo?
TEMA 9
FUNCIONES MATEMÁTICAS
Una función es una relación entre dos magnitudes que asigna a cada valor de una variable un único valor de la otra.
Para establecer la relación que supone una función se pueden utilizar varios métodos:
- Mediante un enunciado: ejemplo:"el coste de las llamadas es de 20 céntimos el minuto" establece larelación entre coste y tiempo de llamada.
- Mediante una tabla: ejemplo: Tiempo(min) 1 2 3 4 5 6
- Coste( cént de €) 20 40 60 80 100 120
- Mediante una fórmula: llamando C al coste y t al tiempo, la relación entre ambos vendría dada por la siguiente fórmula:
- C = 20t
- Mediante una gráfica: utilizaremos dos ejes perpendiculares llamados ejes de coordenadas y en cada uno de ellos representaremos una de las magnitudes. Escribiremos primero su coordenada horizontal (abscisa) y a continuación su coordenada vertical (ordenada).
En todas las funciones tenemos que establecer la relación entre dos magnitudes que reciben el nombre de variables.
La primera de ellas, cuyo valor podemos escoger libremente, se denomina variable independiente y se representa siempre en el eje horizontal.
La segunda, cuyo valor está determinado por la elección de la primera, se denomina variable dependiente y se representa en el eje vertical.
CARACTERÍSTICAS DE UNA FUNCIÓN
- DOMINIO: es el conjunto de valores que puede adoptar la variable independiente.
- CRECIMIENTO: una función es creciente cuando el valor de la variable dependiente aumenta al aumentar el de la variable independiente.De igual forma si disminuye la función será decreciente.
Los puntos en los que la función pasa de ser creciente a decreciente.
Suscribirse a:
Entradas (Atom)